Adaptive Risk Sensitive Path Integral for Model Predictive Control via Reinforcement Learning
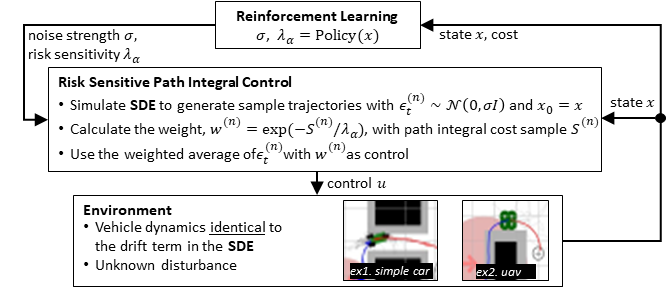
We propose a reinforcement learning framework where an agent uses an internal nominal model for stochastic model predictive control (MPC) while compensating for a disturbance. Our work builds on the existing risk-aware optimal control with stochastic differential equations (SDEs) that aims to deal with such disturbance. However, the risk sensitivity and the noise strength of the nominal SDE in the risk-aware optimal control are often heuristically chosen. In the proposed framework, the risk-taking policy determines the behavior of the MPC to be risk-seeking (exploration) or risk-averse (exploitation). Specifically, we employ the risk-aware path integral control that can be implemented as a Monte-Carlo (MC) sampling with the fast parallel simulations using a GPU. The MC sampling implementations of the MPC have been successful in robotic applications due to its real-time computation capability. The proposed framework that adapts the noise model and the risk sensitivity outperforms the standard model predictive path integral in simulation environments that have disturbances.
UAV Simulation with Double Integrator Kinematics
UGV Simulation with Bicycle Kinematics
Relevant Paper:
- Hyung-Jin Yoon, Chuyuan Tao, Hunmin Kim, Naira Hovakimyan, Petros Voulgaris, “Sampling Complexity of Path Integral Methods for Trajectory Optimization,” IEEE American Control
Conference (2022 ACC) - Chuyuan Tao, Hunmin Kim, Hyung-Jin Yoon, Naira Hovakimyan, Petros Voulgaris, “Control Barrier Function Augmentation in Sampling-based Control Algorithm for Sample Efficiency,”
IEEE American Control Conference (2022 ACC) - Chuyuan Tao, Hyung-Jin Yoon, Hunmin Kim, Naira Hovakimyan, Petros Voulgaris, “Path Integral Methods with Stochastic Control Barrier Functions,” IEEE Conference on Decision and Control (2022 CDC)
- Yoon, Hyung-Jin, et al. “Adaptive Risk Sensitive Path Integral for Model Predictive Control via Reinforcement Learning.” 2023 31st Mediterranean Conference on Control and Automation (MED). IEEE, 2023.