Problem Description
Prim’s algorithm uses the greedy approach to connect n points in the cheapest possible way to make a path.
The greedy approach suggests a “greedy” grab of the best alternative available in the hope that a sequence of optimal choices will yield an optimal solution to the whole problem. “Jump as close to the goal as possible on each move!”
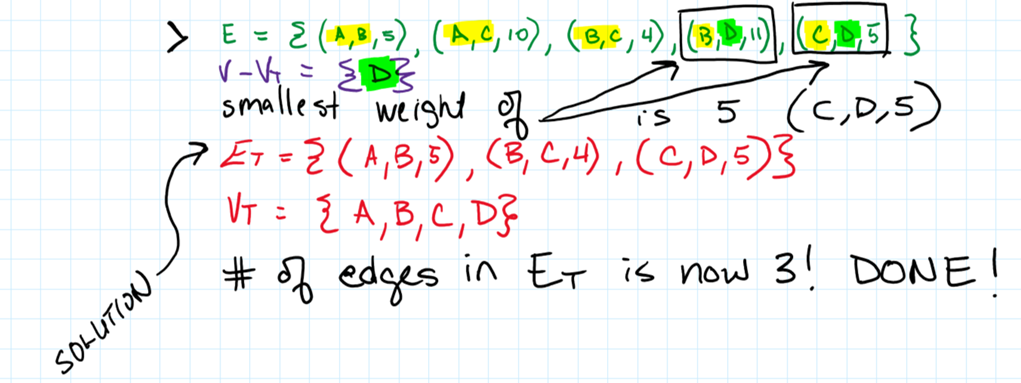
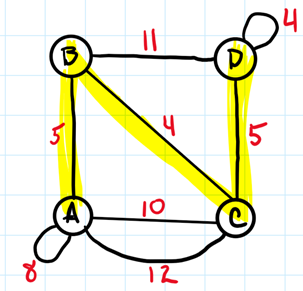
Prim’s algorithm solves the minimum spanning tree problem.
A spanning tree is a subset of an undirected connected graph. This subset is a connected acyclic tree that contains all vertices of the graph.
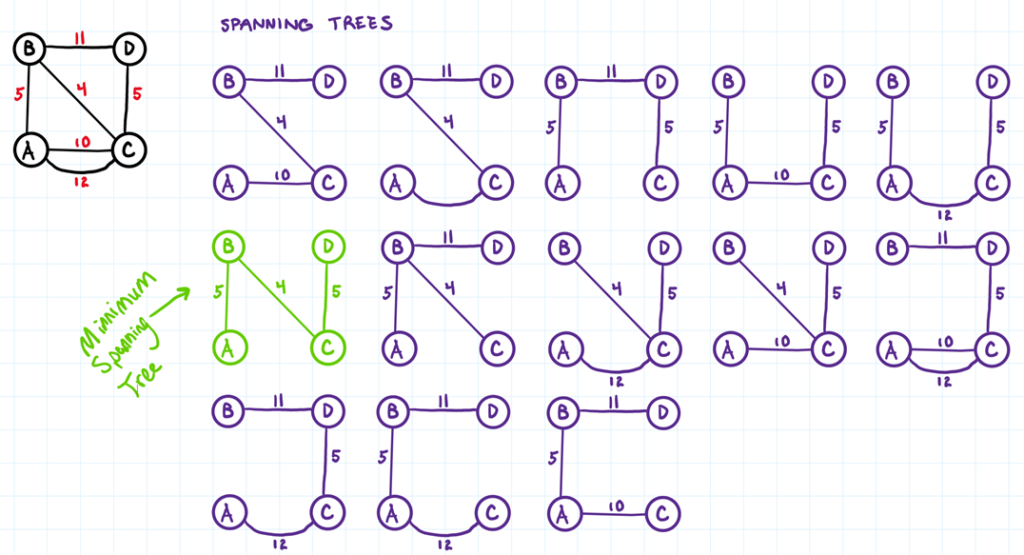
If a graph has weights assigned to its edges, a minimum spanning tree (MST) is a spanning tree that has the smallest weight of all other spanning trees of the graph, where weight is defined as the sum of weights on all edges.
Videos
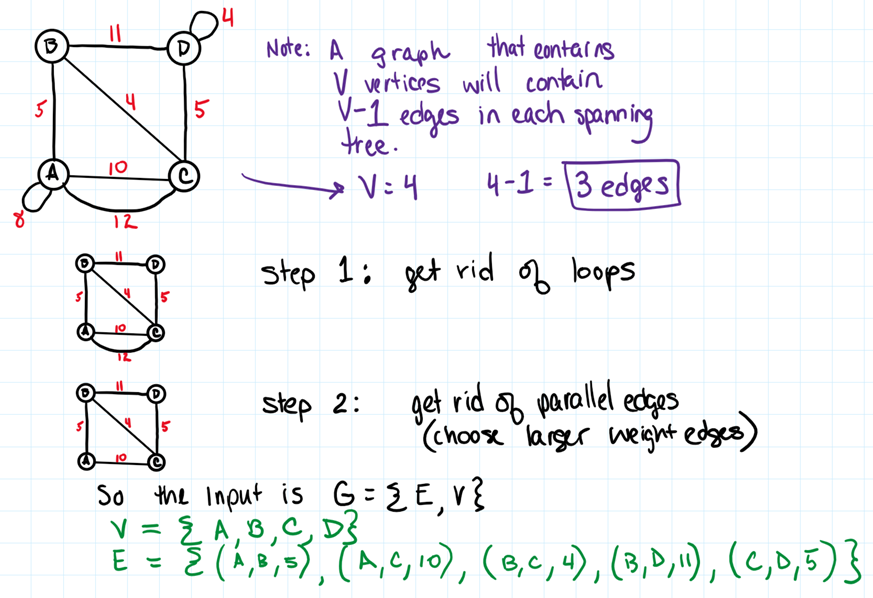
Algorithm Steps Explained with Given Input


Time Efficiency
•The time efficiency of Prim’s algorithm depends on the data structures used to implement the algorithm.
•Using a weight matrix & priority queue array, the efficiency is Θ(|V|2)
•Using a weight matrix & minimum heap, the effiency is O(|E| log|V|)