Problem Description
The Horspool’s algorithm is an algorithm for finding a substring (called a pattern) inside of a string (called a text). The pattern length is m and the text length is n.
Horspools is a simplification of the Boyer-Moore string search algorithm and requires taking up more space (memory) in order to save on time. This is done by making a Bad-Match or Shift Table.
Videos
Algorithm Steps on Sample Input
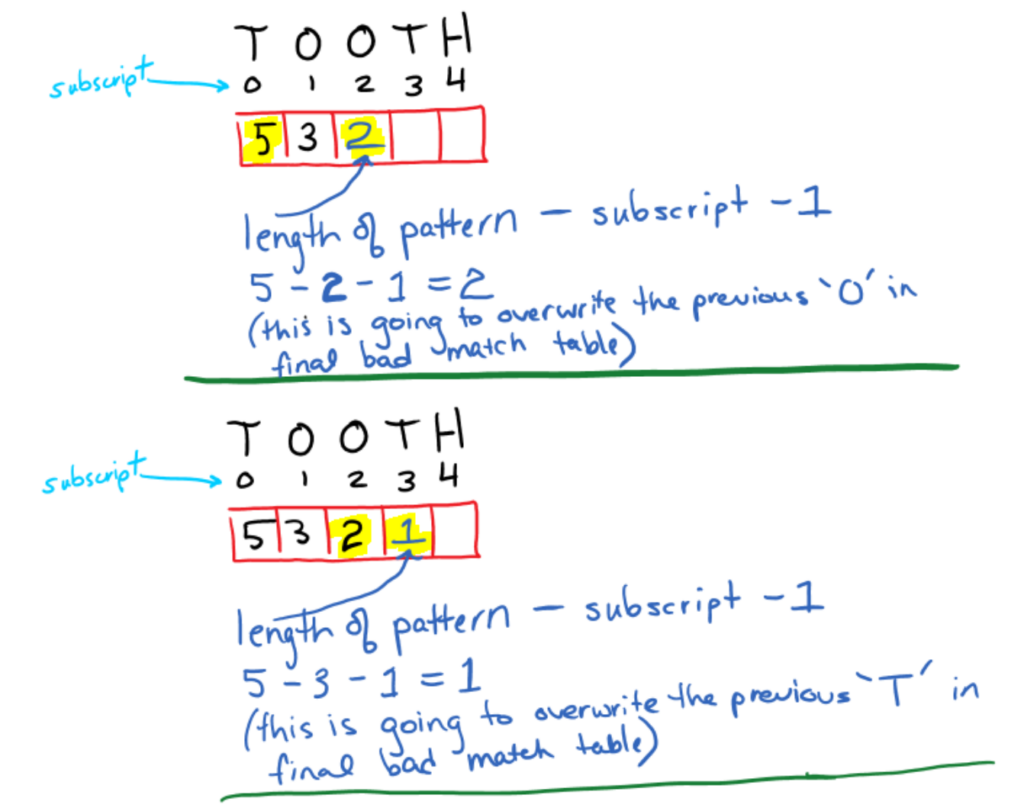
Example Pattern: “TOOTH”
Example Text: “TRUSTHARDTOOTHBRUSHES”
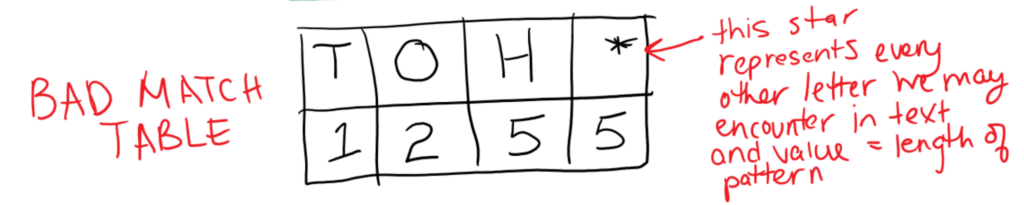
Step 1 – construct bad match table(this is our input enhancement)
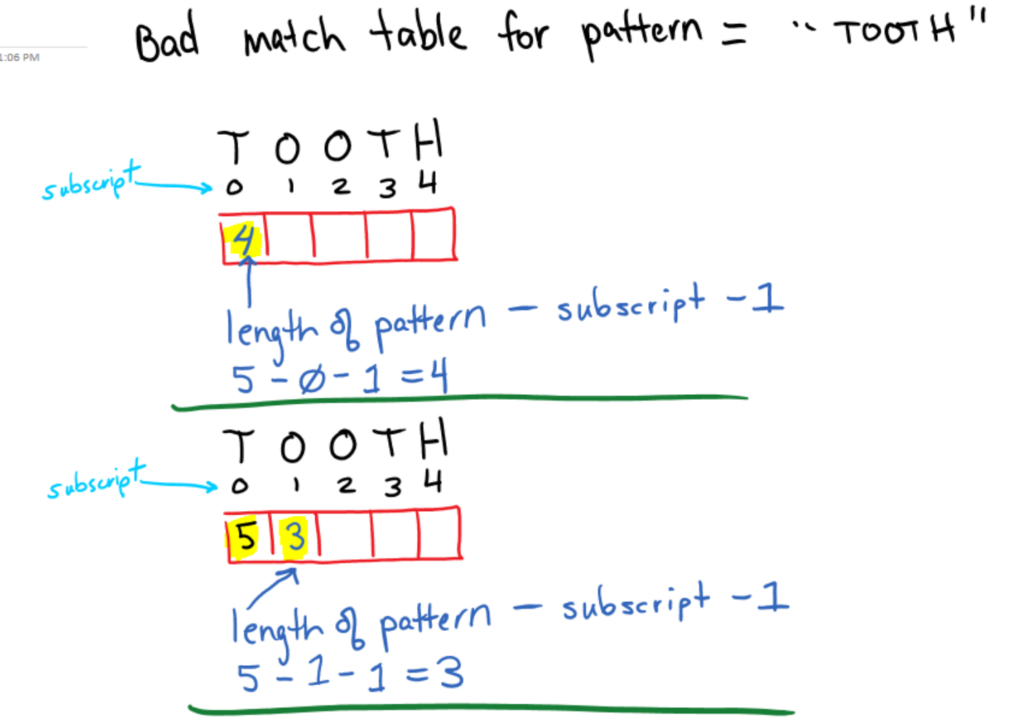

Step 2 – Compare pattern to text using bad match table to determine alignments




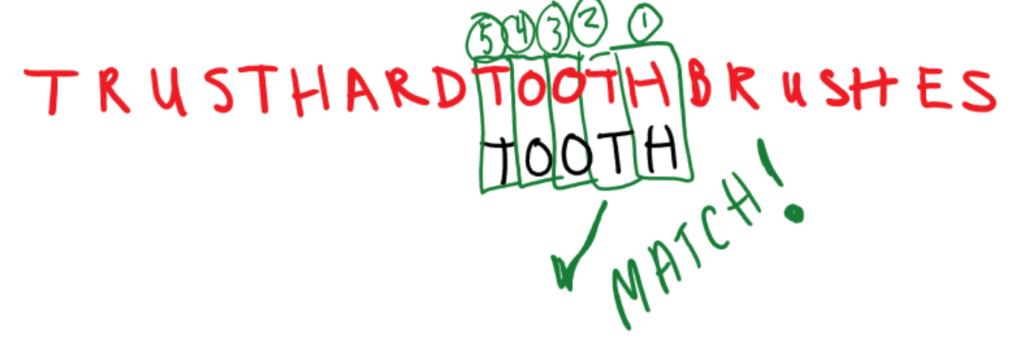
The algorithm is done when either the pattern successfully matches in the text or the pattern moves to the end of the text and no match is found.
Algorithm Pseudocode
Algorithm: Horspool
Input: text T = T[0 . . . n), pattern P = P[0 . . . m)
Output: position of the first occurrence of P in T
Preprocess:
(1) for c ∈ Σ do shif t[c] ← m
(2) for i ← 0 to m − 2 do shif t[P[i]] ← m − 1 − i
Search:
(3) j ← 0
(4) while j + m ≤ n do
(5) if P[m − 1] = T[j + m − 1] then
(6) i ← m − 2
(7) while i ≥ 0 and P[i] = T[j + i] do i ← i − 1
(8) if i = −1 then return j
(9) j ← j + shif t[T[j + m − 1]]
(10) return n
Time Efficiency/Complexity
The Worst Case efficiency is O(nm) where n is the text length and m is the pattern length.
The Average Case efficiency is O(n) where n is the text length
Although in the same efficiency class as brute force in worst case, Horspool’s algorithm is obviously faster on average because of being able to shift more than one space at a time.